Les paradoxes de Zénon : La pensée grecque ancienne face aux mathématiques modernes
Les paradoxes de Zénon, philosophe grec du Ve siècle avant J.-C., sont restés une énigme fascinante pendant des siècles. Ils questionnent des concepts fondamentaux comme le mouvement, le temps et l’infini. À travers plusieurs exemples, Zénon a cherché à montrer que notre intuition sur ces concepts pouvait être trompeuse. Ces paradoxes ont intrigué des générations de penseurs et, bien que les mathématiques modernes aient permis de les résoudre en partie, ils continuent de susciter des discussions philosophiques.
Dans cet article, nous allons explorer trois des plus célèbres paradoxes de Zénon et comprendre comment ils remettent en question notre perception du mouvement et de l’infini.
Le paradoxe d’Achille et de la tortue
Ce paradoxe est probablement le plus célèbre. Il illustre une situation où Achille, un héros grec rapide, doit courir contre une tortue lente. Imaginons qu’Achille donne un avantage de départ à la tortue. Zénon soutient qu’Achille ne pourra jamais rattraper la tortue, même s’il court beaucoup plus vite. Voici pourquoi :
- Au début, la tortue est à une certaine distance devant Achille.
- Quand Achille atteint la position initiale de la tortue, celle-ci a avancé un peu plus loin.
- Quand Achille atteint cette nouvelle position, la tortue a encore avancé, et ainsi de suite.
Zénon conclut que, puisqu’il y a toujours une distance à franchir, aussi petite soit-elle, Achille ne rattrapera jamais la tortue. Le paradoxe soulève une question sur la façon dont nous comprenons la notion de distance et de temps, et comment une somme infinie de petites distances peut avoir une durée finie.
Résolution moderne : la série infinie
Les mathématiques modernes, avec la notion de séries infinies, résolvent ce paradoxe. Bien que le nombre de segments que doit parcourir Achille soit infini, la somme des temps nécessaires pour parcourir chaque segment diminue progressivement et finit par être finie. En d’autres termes, si Achille court à une vitesse constante et la tortue à une vitesse plus lente, Achille rattrapera la tortue en un temps déterminé. Ce concept est expliqué par la somme des séries géométriques convergentes.

Le paradoxe de la flèche
Dans ce paradoxe, Zénon s’intéresse à la nature du mouvement. Imaginez une flèche en plein vol. Zénon affirme que, si vous considérez un instant précis dans le temps, la flèche, à ce moment exact, n’est ni en mouvement ni immobile. Si elle n’est pas en mouvement pendant un seul instant, alors comment peut-elle bouger à travers tous les instants successifs ?
Zénon en conclut que, puisque le temps est constitué d’instants individuels et que la flèche est immobile à chaque instant, le mouvement est une illusion.
Résolution moderne : le calcul différentiel
Le paradoxe de la flèche peut être résolu en termes de calcul différentiel, une branche des mathématiques qui traite des variations infinitésimales. Le mouvement est défini comme le changement de position dans le temps, mais cela ne signifie pas que la flèche doit « bouger » à chaque instant. Le calcul différentiel permet de définir la vitesse comme une limite, ce qui signifie que même si la position de la flèche est « fixe » à chaque instant, sa vitesse globale est non nulle et le mouvement est bien réel.
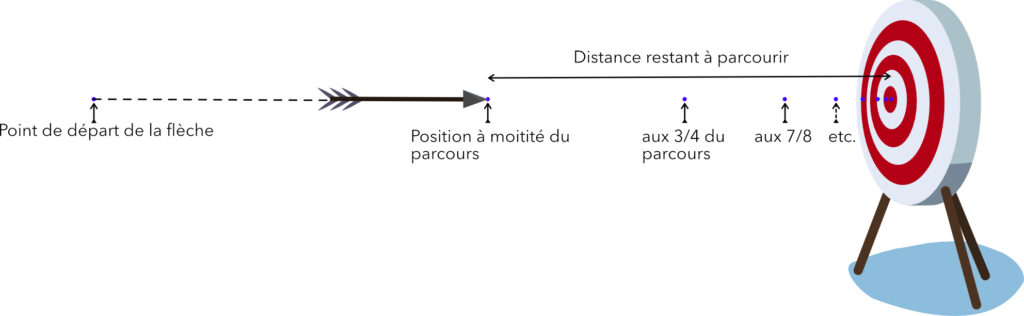
Le paradoxe de la dichotomie
Le paradoxe de la dichotomie se concentre sur l’idée qu’avant d’atteindre un point donné, un objet en mouvement doit d’abord atteindre la moitié de la distance qui le sépare de ce point. Ensuite, il doit parcourir la moitié de la distance restante, et ainsi de suite, à l’infini. Zénon soutient que cela implique qu’il est impossible de parcourir la distance complète, car il y a toujours une autre moitié à franchir.
Résolution moderne : les limites mathématiques
Comme pour le paradoxe d’Achille et de la tortue, les mathématiques modernes résolvent ce paradoxe en utilisant le concept de limite. Bien que le nombre de divisions soit infini, la somme totale de ces divisions reste finie. Cela signifie qu’un objet peut, en effet, parcourir une distance finie même s’il semble devoir franchir une infinité d’étapes.
La pensée de Zénon dans le contexte moderne
Les paradoxes de Zénon sont restés des casse-têtes philosophiques jusqu’à l’avènement du calcul infinitésimal par Isaac Newton et Gottfried Wilhelm Leibniz au XVIIe siècle. Ce nouvel outil mathématique a permis de manipuler des concepts d’infini d’une manière précise, en introduisant des notions telles que les dérivées et les intégrales, qui sont utilisées pour comprendre des quantités infiniment petites.
En utilisant ces concepts, les mathématiques modernes ont montré que les paradoxes de Zénon sont le résultat d’une mauvaise interprétation du concept d’infini. Alors que Zénon voulait prouver que le mouvement était impossible, nous comprenons aujourd’hui que le mouvement et l’infini peuvent coexister, grâce aux concepts de limites et de convergence.

Conclusion
Les paradoxes de Zénon continuent de fasciner parce qu’ils remettent en question nos intuitions sur des concepts aussi fondamentaux que le mouvement, le temps et l’infini. Bien que la science moderne ait résolu ces paradoxes d’un point de vue mathématique, ils restent un sujet de réflexion profond pour les philosophes. Zénon, avec sa pensée audacieuse, a réussi à prouver que parfois, ce que nous percevons comme évident mérite d’être questionné de manière plus rigoureuse.